In our regular life we can see many types of figures/ shapes/structures. A simple closed figure which is formed by three or more lines or more than three lines is called a polygon.
If a polygon has n-sides then it is said to be N-gon. i.e. for example see the below polygon it has 4 sides and it is said to be 4-gon.

Diagonal of a polygon:- A line segment which is joining any two non-consecutive vertices of a polygon is called its diagonal. Observe the Figure-1 Here A and C joins with a line segment AC like wise BD also so here AC,BD are called Diagonal of the polygon.
Here Vertices are A,B,C and D.
To find the No.of diagonal of a n-sided polygon we can use the below formula
[n(n-3)]/2 here n is no of sides of the polygon.
Consider the above figure we have n is 4 here and substitute the n value as 4 here then we get 2.
Polygons are basically Two types those are:
1. Convex polygon
2. Concave polygon
Convex polygon: In this type of polygon each angle is measured less than 180 degrees means two right angles such a polygon is called convex polygon.

Concave polygon: In this type of polygon if an angle is measured 180 degrees means two right angles such a polygon is called concave polygon.

Angle between two sides of polygon
Angles of a polygon: Basically polygons having two types of angles those are Exterior and interior angles.

Interior angle Exterior angle:
An angle inside the polygon is called the interior angle (Green color i the picture) and an angle outside of the polygon is called exterior angle(Red color in the Picture).
Note 1:
Sum of the outside angle of polygon is 360 degrees.
Each exterior angle is measured by using 360/n here n is side of the polygon.
Note 2:
Sum of interior angle of a polygon is (n-2)*180 degrees. here n is side of the polygon.
Each interior angle is measured by using [(n-2)*180]/n , here n is side of the polygon.
- For example a polygon has 5 sides then find the each exterior and interior angle and sum of the interior and exterior angle.
- Sum of exterior angle is =360 degrees.
- Sum of interior angle is (n-2)*180 here n is 5
(5-2)*180=540 degrees. - Each exterior angle is 360/n n is 5 here so 360/5=72 degrees.
- Each interior angle is [(n-2)*180]/n here n is 5 so by using formula we get 108 degrees.
- Apart from this polygons are divide into two those are Equilateral and Equiangular.
- A polygon in which all sides are equal then is called equilateral polygon . example is Rhombus.
- A polygon in which all angles are equal then is called equiangularl polygon . example is rectangle.
The Basic rule to form a polygon is It is closed figure which is having three or more lines.
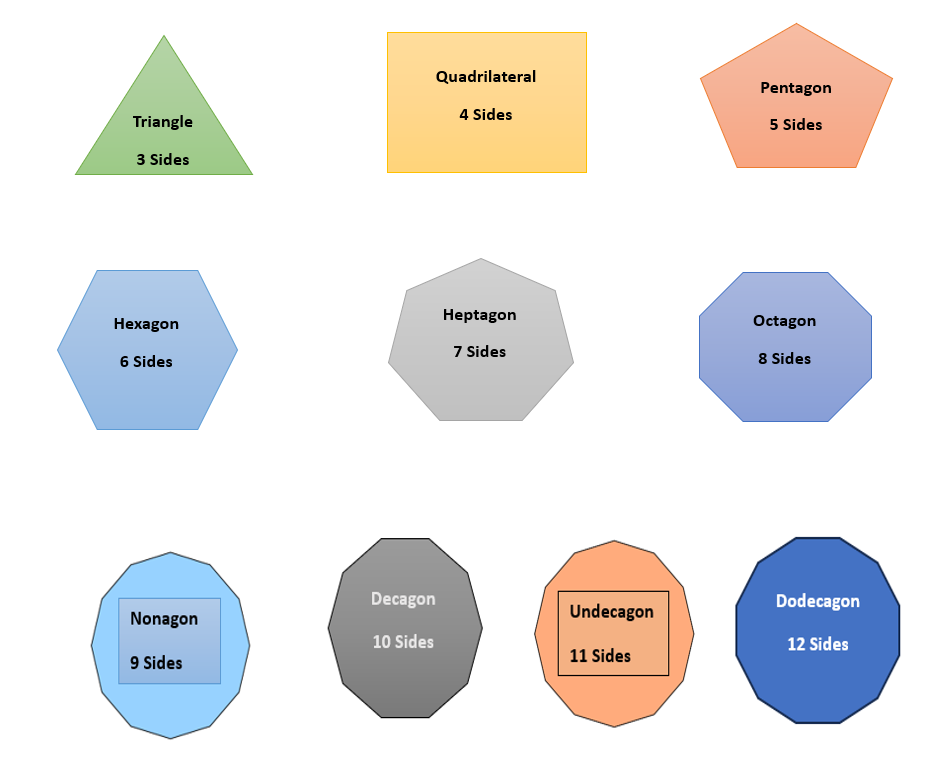
If a polygon is having Three sides It is called as Triangle.
If a polygon is having four sides it is called as Quadrilateral.
If a polygon is having five sides it is called as Pentagon.
If a polygon is having six sides It is called as Hexagon.
If a polygon is having seven sides it is called as Heptagon.
If a polygon is having eight sides it is called as Octagon.
If a polygon is having nine sides It is called as Nonagon.
If a polygon is having ten sides it is called as Decagon.
If a polygon is having eleven sides it is called as undecagon and endecagon or Hendecagon.
If a polygon is having twelve sides it is called as Dodecagon.
 IT2EDU Empowering Education Through Technology
IT2EDU Empowering Education Through Technology