Merge Sort

Merge Sort is a sorting technique based on divide and conquer technique with comparison.

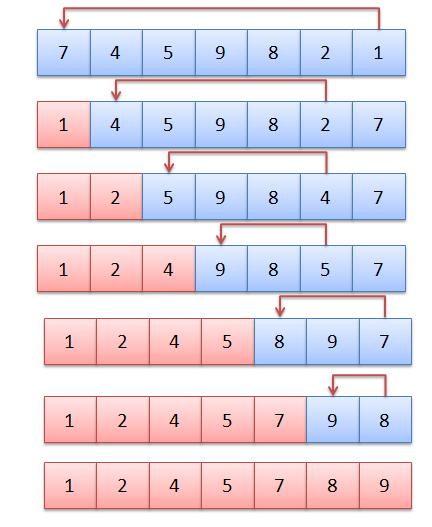
Conceptually, a merge sort works as follows :

i) Divide the unsorted list into n sublists, each containing 1 element (a list of 1 element is considered sorted).

ii) Repeatedly merge sublists to produce new sublists until there is only 1 sublist remaining. This will be the sorted list.

Worst Case performance: O (n log n)
Best case Performance: O (n log n) for typical O(n) natural variant
Average performance: O(n log n)
Worst case space complexity : O(n)

Merge Sort Pseudocode and Algorithm:

MergeSort (Array(First..Last))
Begin
If Array contains only one element Then
Return Array
Else
Middle= ((Last + First)/2) rounded down to the nearest integer
LeftHalfArray = MergeSort(Array(First..Middle))
RightHalfArray = MergeSort(Array(Middle+1..Last))
ResultArray = Merge(LeftHalfArray, RightHalfArray)
Return ResultArray
EndIf
End MergeSort

Java Program for Merge Sort:

import java.util.Scanner;

public class MergeSort

{

public static void sort(int[] a, int low, int high)

{

int N = high – low;

if (N <= 1)

return;

int mid = low + N / 2;

sort(a, low, mid);

sort(a, mid, high);

int[] temp = new int[N];

int i = low, j = mid;

for (int k = 0; k < N; k++)

{

if (i == mid)

temp[k] = a[j++];

else if (j == high)

temp[k] = a[i++];

else if (a[j] < a[i])

temp[k] = a[j++];

else

temp[k] = a[i++];

}

for (int k = 0; k < N; k++)

a[low + k] = temp[k];

}

public static void main(String[] args)

{

Scanner scan = new Scanner(System.in);

System.out.println(“Merge Sort Testn”);

int n, i;
System.out.println(“Enter number of integer elements”);

n = scan.nextInt();
int arr[] = new int[n];
System.out.println(“nEnter ” + n + ” integer elements”);

for (i = 0; i < n; i++)

arr[i] = scan.nextInt();

sort(arr, 0, n);
System.out.println(“nElements after sorting “);

for (i = 0; i < n; i++)

System.out.print(arr[i] + ” “);

System.out.println();

}
}